Elektromagnetické javy a ich miesto v elektronike

úvaha 26-30 |
|
OBSAH
26. Sily pôsobiace na náboje a prúdy v magnetickom poli
27. Skutočne magnetické sily nikdy nekonajú prácu? - (1)
28. Skutočne magnetické sily nikdy nekonajú prácu? - (2)
29. Superstabilizácia frekvencie reflexného klystrónu
30. Niekoľko slov na prelome rokov!
_____________________________________________________________________________
26. Sily pôsobiace na elektrické náboje a prúdy v magnetickom poli
Magnetické sily a silové pôsobenia sa vo fyzikálnej obci často démonizujú, dovolľujem si preto do problematiky vniesť vlastný názor.
V elektromagnetizme sú zavedené dve magnetické sily – magnetická časť Lorentzovej sily a Ampérova sila. Lorentzova sila je všeobecná elektromagnetická sila Felmag = QE + Qv × B, ktorou elektromagnetické pole pôsobí na pohybujúci sa náboj Q v elektromagnetickom poli a Ampérova sila dFA = Idl × B, ktorou magnetické pole pôsobí na elementárny úsek prúdovodiča dl, ktorým tečie elektrický prúd I. Hoci tieto sily majú spoločný pôvod, ich účinky sa diametrálne líšia. Pozrieme sa najprv na účinok magnetickej časti Lorentzovej sily:
Ak sa voľná častica (náboj Q s hmotnosťou m) s rýchlosťou v ocitne vo voľnom priestore v homogénnom magnetickom poli indukcie B kolmo na jeho smer, potom sa v priestore bude pohybovať po kruhovej dráhe polomeru r = mv/(QB) s cyklotrónovou frekvenciou wc = QB/m pod účinkom dostredivej sily
FL = Qv × B (1)
(pozri obr. 1). Tato sila je magnetickou časťou elektromagnetickej sily Felmag a budeme ju nazývať Lorentzovou silou, hoci je iba časťou tejto sily. Takto chápaná Lorentzova sila nikdy nevykonáva na častici žiadnu prácu, pretože je kolmá na smer jej rýchlosti.
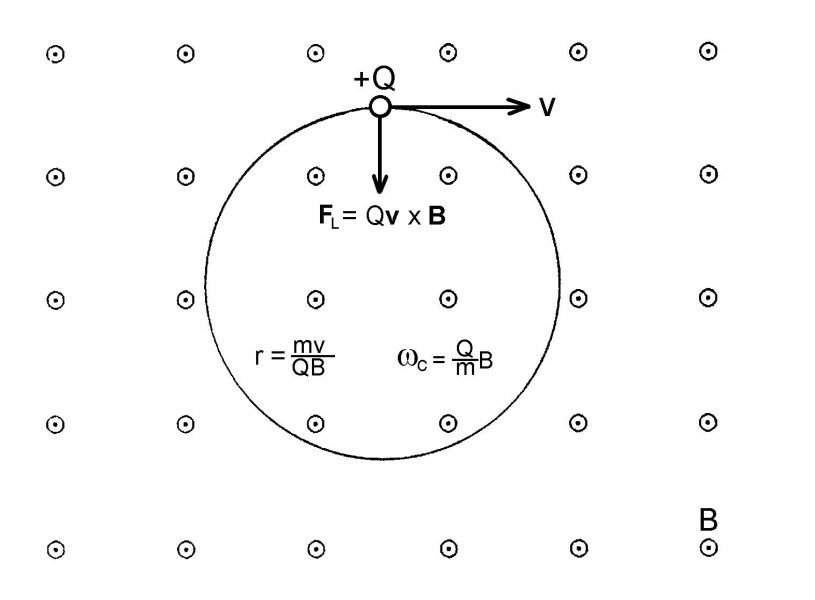
Obr. 1
Keby nebolo magnetického poľa častica by sa samozrejme pohybovala priamočiaro konštantnou rýchlosťou v. Kruhový pohyb nanucuje častici magnetické pole B. Je len samozrejmé, že dostredivá sila nekoná žiadnu prácu, tak ako sa nekoná práca pri pohybe elektrónu v klasickom (nie v kvantovomechanickom) vodíkovom atóme a tiež pri pohybe satelitu okolo planéty. (Tu si treba dať ale pozor – elektrické a gravitačné sily sú konzervatívne sily, zatiaľ čo magnetická sila je nekonzervatívna, niekedy nazývaná vírová, alebo solenoidálna sila, ale silový účinok je vo všetkých troch prípadoch rovnaký – práca sa nekoná). Treba si tiež uvedomiť, že Lorentzova sila je relativistická sila, závislá od rýchlosti, treba preto brať do úvahy všetky dôsledky tohto faktu. Lorentz ju sformuloval ako dôsledok relativistických transformácii elektromagnetických polí (pozri „Elektromagnetizmus“, odsek 6.5, prípadne aj úvahu 21).
Iná je situácia, ak je súbor elektrických nábojov súčasťou vodivého materiálu (napr. tenkého ideálne vodivého drôtu) ak sa v ňom udržuje elektrický prúd I. Smer prúdu nábojov hnaných zdrojom EMN (budeme predpokladať, že sa jedná o kladné náboje) je diktovaný orientáciou prúdovodiča a prúdová dráha nie je nutne kružnica predpísaného polomeru r a neodpovedá pohybu podľa výrazu (1), častice sa snažia pohybovať po predpísanej kružnici od Lorenzovej sily, ale z vodiča vystúpiť nemôžu. V takom prípade pre silu, ktorá pôsobí sprostredkovane na úsek prúdovodiča Idl a nie priamo na náboje, platí výraz (Ampérova sila)
dFA = Idl × B (2)
(pozri obr. 2). Prúd I v obvode udržuje zdroj elektromotorického napätia (EMN – napr. galvanický článok, jednosmerný generátor napätia a pod.), pričom náboje sa vo vodiči pohybujú driftovou, konštantnou rýchlosťou vd (pozri obr. 2c). Rýchlosť vd je konštantná preto, lebo v obvode je odpor, ktorý vytvára „treciu“, brzdnú silu, opačnú ako je hnacia sila zdroja EMN, dFe ktorá núti náboje prekonávať odporovú bariéru, bez brzdnej sily by sa náboje vo vodiči pohybovali so zrýchlením. Pri pohybe nábojov v prúdovodiči (v drôte) pôsobí na ne priečna Lorentzova sila (na obr. 2a zdola nahor), kladné náboje sa posúvajú priečne nahor, dole vzniká ich nedostatok, pretože vodič je ináč elektricky neutrálny. Vo vodiči takto vzniká Hallov jav (pozri odsek 8.5.2 citovanej učebnice), vzniká v ňom intenzita elektrického poľa EH a s ňou spojene Hallovo napätie UH. Hallova intenzita nepôsobí silovo na vodič, preto si ju v ďalšom nebudeme všímať. Treba si ale uvedomiť, že práve proti „Hallovej sile“ od plášťa vodiča pôsobí Lorentzova sila na náboje vo vodiči. Ampérová sila (2), pôsobí mechanickým tlakom, alebo ťahom na vodič a snaží sa ho vyviesť zo svojej polohy.
V mnohých učebniciach sa výraz (2) nerozmyslene integruje po dráhe l časti prúdovodiča, alebo po uzavretej dráhe, čo nepovažujem za správne. Sila je vektorová veličina, ktorá musí mať lokalizované svoje pôsobisko a z takého integrálu, ktorý je vlastne vektorovým integrálnym súčtom elementárnych síl nevidieť, kde na prúdovej dráhe sila pôsobí. Situácia by sa ešte viac skomplikovala, ak by sa integrál mal počítať po uzavretej dráhe l (!) (veď musíme mať na pamätí, že stacionárne prúdy musia tiecť po uzavretých vodivých krivkách). Vtedy by už vôbec nebolo jasné, kde tá sila pôsobí a aký má význam. Podobné pochybné výrazy sa objavujú v mnohých, ináč múdrych učebniciach, keď autor v zápale práce si neuvedomuje, čo píše – keď ten integrál tak pekne vyzerá! Tu namiesto síl treba uvažovať točivé momenty magnetických síl na prúdový obvod, ktoré by boli nenulové (pozri napr. odsek 6.4.2 cit. učebnice), alebo zostať pri silovom pôsobení podľa výrazu (2).
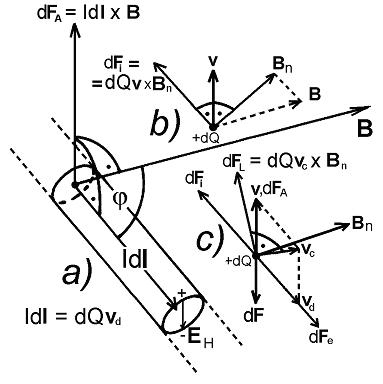
Obr. 2
Pozrime sa teraz na prúdový element Idl z iného hľadiska (obr. 2c). Element Idl sa pohybuje rýchlosťou v a náboje v ňom sa pohybujú driftovou rýchlosťou vd. Ak tieto rýchlosti vektorovo sčítame na rýchlosť vc = v + vd, potom kolmo na rýchlosť vc možno zkonštruovať „Lorentzovu silu“ dFL = dQvc × B pôsobiacu na nábojový element dQ v objeme elementárneho prúdovodiča. Ale pozor – je toto legálne, že si kolmo k smeru rýchlosti vymyslime silu? Táto vymyslená sila kolmá na „rýchlostný hybrid vc“ by skutočne nemala konať žiadnu prácu. Tak sa totiž uvažuje v mnohých učebniciach! Silu dFL možno ale rozložiť na jej zložky (pozdĺž elementu Idl a kolmo naň), ktoré s prácou súvisia. Pozdĺž elementu je to sila elektromagnetickej indukcie dFi a kolmo na element Ampérová sila (magnetická!) dFA. Sila dFi kompenzuje hnaciu silu dFe zdroja EMN tak, aby rýchlosť vd ostala konštantná a Ampérova sila dFA kompenzuje vonkajšiu (brzdnú) silu dF, aby aj rýchlosť v ostala konštantnou (pozri obr. 2c). Či možno v takej situácii hovoriť, že magnetické sily nikdy nekonajú prácu, to už nech každý posúdi sám! Záverom možno povedať, že silové pôsobenie na prúdy v magnetickom poli je veľmi zložité, ale všetky pôsobiace sily okrem sily zdroja EMN a vonkajšej, mechanickej sily majú pôvod v Lorentzovej sile (1). Na voľné náboje v magnetickom poli Lorentzova sila pôsobí tak, že zakrivuje ich dráhy, ale nikdy nevykonáva na nich prácu. Ampérova sila, pôsobiaca na prúdovodiče pretekané prúdmi v magnetickom poli, môže spôsobiť posun prúdovodičov v poli a teda môže na nich prácu vykonávať. Sila elektromagnetickej indukcie vytvára pozdĺž vodiča indukované elektromotorické napätie a indukované prúdy v súhlase s Lenzovym pravidlom a nakoniec sila elektromagnetickej indukcie priamo na náboje priečne vo vodiči (Hallov jav), vytvára vo vodiči priečne Hallovo napätie UH s Hallovou intenzitou EH. Po dlhšom čase Vás všetkých pekne pozdravujem a želám všetko príjemné! Autor
05.08.2009
27. Skutočne magnetické sily nikdy nekonajú prácu? - (1)
Keď počujem tvrdenie, že magnetické sily nikdy prácu nekonajú – okamžite si kladiem otázku: Ako teda pracujú veľké elektromagnety, ktoré prenášajú ťažké bremená, elektrické točivé stroje (elektromotory, dynama) atď.? Ako funguje vysokofrekvenčný ohrev a magnetické brzdy? Dostanem asi odpoveď, že magnetické polia, ktoré túto prácu vykonávajú, sú dôsledky elektrických prúdov, ktoré ich vytvárajú a tie prácu vykonávajú na úkor energie zdrojov elektromotorických napätí, alebo na účet vnútornej energie permanentných magnetov. V poriadku, ale práve takáto je filozofia zavedenia pojmu „magnetizmus“ – je to silový odraz pohybu elektrických nábojov, alebo toku elektrických prúdov v priestore a magnetické pole je ich prostredníkom! (Je známe, že náboj q, ktorý sa pohybuje v priestore rýchlosťou v vytvára vo vektorovej vzdialenosti r magnetickú indukciu B = (µ0/4pi)qv × r/r3 (pi = 3,14159..... je Ludolfovo číslo) – pozri napr. „Elektromagnetizmus“, odsek 6.1.1). Možno že nedorozumenia vznikajú práve neuvedomením si tejto skutočnosti, či terminológiou.
Poďme po poriadku! Ako je dobre známe (pozri napr. vyššie citovanú učebnicu, odseky 7.7 až 7.9) magnetic-
ké pole má energiu, ktorej objemová hustota je
wm = B2/(2µ) [J.m-3]
(µ je magnetická konštanta, prípadne permeabilita prostredia) a keďže táto energia sa môže meniť, môže a musí sa to diať iba tak, že magnetické pole prácu vykonáva, alebo ju prijíma.
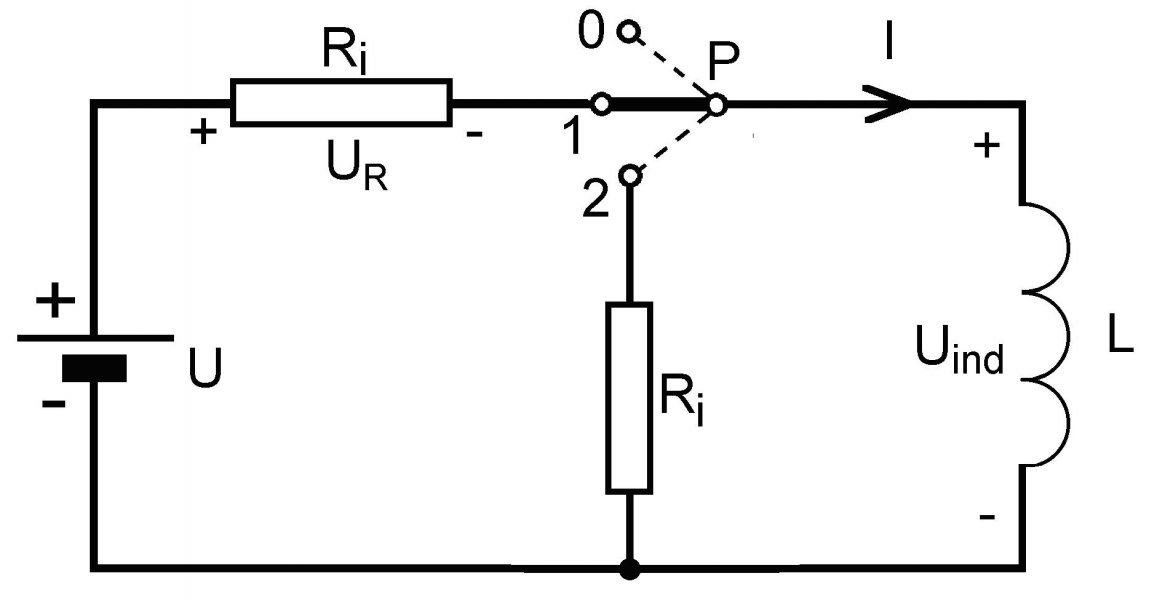
Obr. 1
Pokúsme sa niektoré vlastnosti síl magnetických polí posúdiť tak povediac – od podlahy. Predovšetkým preskúmajme vlastnosti elektrického obvodu na obr. 1, kde ukážeme, že zmena magnetickej energie je spojená s prácou. Keď sa zapne prepínač P z polohy 0 do polohy 1 v obvode začne pôsobiť zdroj elektromotorického napätia (EMN) U s vnútorným odporom Ri pripojený k indukčnosti L (indukčnosť tvorí napr. jednovrstvová valcová cievka – solenoid). V obvode tečie elektrický prúd I, ktorý v okamihu zapnutia prepínača P do polohy 1 stúpa exponenciálne z nulovej hodnoty a po teoreticky nekonečnej dobe (prakticky po dobe asi 5L/Ri - čo je päťnásobok časovej konštanty obvodu) dosiahne asymptotickú hodnotu I∞ = U/Ri(bez prítomnosti indukčnosti by prúd stúpol okamžite na hodnotu I∞). Položme si otázku aká energia zo zdroja sa spotrebuje za nekonečne dlhý čas. Spotrebovaná energie bude samozrejme nekonečná, pretože zdroj po doznení prechodového javu kúri do odporu s konštantným výkonom RiI∞2 wattov.
Zaujímavejšie je, čo sa deje v indukčnosti, v solenoide. Výpočet v odseku 7.7 citovanej učebnice ukazuje, že v indukčnosti, za nekonečne dlhý čas, pri konečnom, stacionárnom prúde I∞ sa uloží vo forme magnetického poľa len konečná potenciálna magnetická energia veľkosti Wm = (1/2)LI∞2= (1/2)FiI∞, kde Fi= LI∞ je magnetický indukčný tok solenoidom. Kde sa táto energia zobrala? Predsa v prúde, ktorý musel zdroj cez odpor a indukčnosť pretlačiť! Na odpore sa za istý čas časť dodanej energie nevratne premenila na teplo na indukčnosti musel zdroj premáhať indukované EMN veľkosti LdI/dt a tak „pumpoval“ magnetickú energiu do indukčnosti, až na jej konečnú hodnotu Wm.
Druhá otázka znie: Je schopná táto energia vykonať prácu? Ak chceme nájsť odpoveď na túto otázku, prepnime v ustálenom stave prúdu I∞ v obvode prepínač P do polohy 2. Táto operácia na veľkých indukčnostiach (napr. na ťažkých elektromagnetoch) s veľkými prúdmi môže mať pri neopatrnosti dramatické dôsledky. Elektrický obvod indukčnosti sa pri tejto operácii nesmie ani na okamih prerušiť. Ak by sa tak stalo, indukované elektromotorické napätie na indukčnosti LdI/dt, by teoreticky narástlo do nekonečna, prakticky na veľmi veľkú hodnotu (pri okamžitom prerušení prúdu dI/dt → ∞) a to by mohlo viesť k zničeniu veľkej indukčnosti v horšom prípade k ohrozeniu obsluhy. V predchádzajúcich úvahách viackrát citovaný Profesor Purcell v svojej učebnici „Electricity and magnetism“ dramaticky konštatuje: Ľudia zomierali pri rozopínaní obvodov s veľkými indukčnosťami…
Po prepnutí prepínača do polohy 2, v prvom okamihu spojitý prúd I∞ má tendenciu klesať, pokles indukčného toku v čase však okamžite indukuje v cievke elektromotorické protinapätie, ktoré sa snaží udržať prúd v novom obvode a v rovnakom smere. Pod účinkom tohto napätia prúd neklesne okamžite, ale bude k nule klesať exponenciálne s časovou konštantou L/R (pozri odsek 7.9 v cit. učebnici). A tak aj bez vonkajšieho zdroja prúd tečie v obvode s odporom Ri a nevratne odovzdáva odporu tepelná energiu s výkonom RiI2. Aká je celková energia, ktorá sa v odpore premení na teplo? Výpočet ukazuje, že celková práca magnetického poľa odovzdaná odporu Ri je WT = Wm = (1/2)LI∞2 = (1/2)FiI∞, teda práca, ktorá sa rovná energii v indukčnosti v okamihu prepnutia prepínača do polohy 2. No a kde je tu magnetická sila? Je to sila elektromagnetickej indukcie, ktorá ženie náboje cez odpor Ri a tam vykoná tepelnú prácu. Pôvod má v magnetickom poli indukčnosti L. Na vodičoch cievky by sme zistili aj Hallov jav (pozri úvahu 26), ale na závitoch solenoidu je tak zložitý a pre naše úvahy nepodstatný, že si ho v ďalšom nebudeme všímať.
Možno urobiť záver a položiť si otázku: Po prepnutí prepínača do polohy 2 na odpore R sa vykonáva práca, pričom v obvode niet ničoho, okrem magnetického poľa, čo by túto prácu vykonávalo. Sme teda oprávnení tvrdiť, že magnetické pole, alebo magnetické sily nikdy prácu nekonajú?
Jednosmerný lineárny elektrický motor
Pozrime sa teraz na elektrický prúdový obvod na obr. 2 na ktorom pôsobenie magnetických síl je evidentnejšie. V obvode pôsobí ideálny zdroj EMN U pripojený pomocou dvoch zberníc k vodivej tyči hmotnosti m s elektrickým odporom R. Tyč je predbežne pevne pripojená k zberniciam. Okrem odporu R nijakých odporov niet, vodiče sú ideálne vodivé. Obvod je rovinný a kolmo na rovinu obrázka je naložené homogénne magnetické pole indukcie B, pre jednoznačnosť smerujúce za rovinu.
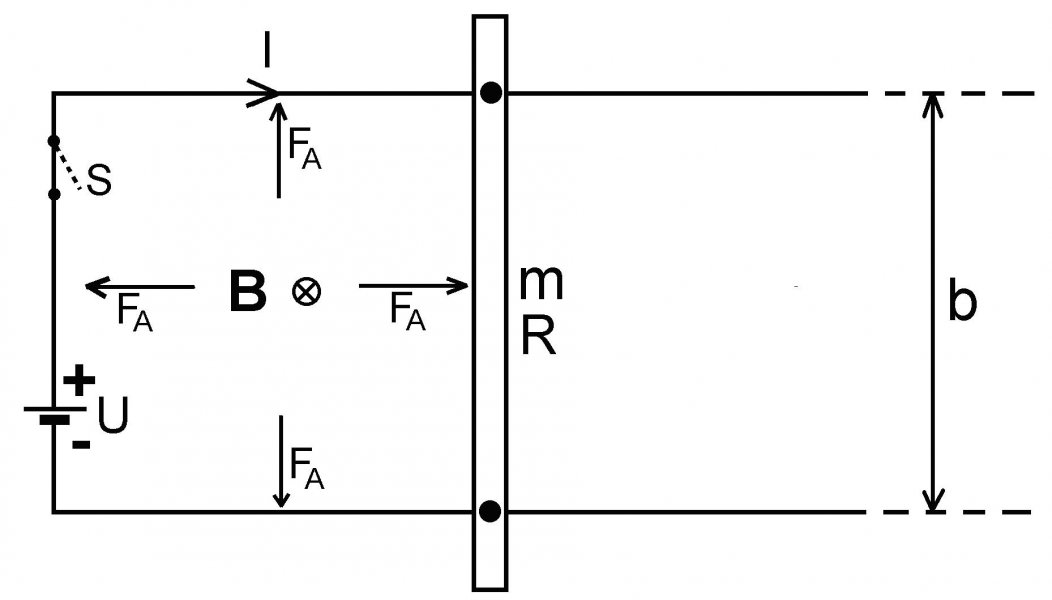
Obr. 2
Po uplynutí dostatočne dlhého času od zopnutia spínača S, keď zanikne prechodový jav súvisiaci s nenulovou indukčnosťou L obvodu, tečie v obvode elektrický prúd I = U/R a pri danom smere prúdu I Ampérove sily FA = IBl na jednotlivých úsekoch obvodu (l sú jednotlivé dĺžky priamych úsekov obvodu, pre kolmé úseky l = b), pôsobiace na jednotlivé časti obvodu sa snažia zväčšiť plochu prúdového obvodu. Ak by bol smer prúdu, alebo magnetického poľa opačný, obvod by mal snahu sa „scvrknúť“. Treba si uvedomiť, že na jednotlivé úseky obvodu pôsobí aj vlastné magnetické pole prúdu (vnútorná magnetická energia obvodu), ktorá sa ho snaží roztrhnúť. Ak by sme sa na obvod dívali ako na elementárnu prúdovú slučku (magnetický „dipól“), je tu analógia s elektrickým dipólom, ktorého vlastne elektrické pole sa tiež snaží „zlikvidovať“ dipól tak, že ho zneutralizuje. V tejto súvislosti je zaujímavé pozrieť si príklad 175 v citovanej učebnici, kde je ukázané, aká veľká magnetická sila napína závit solenoidu s prúdom.
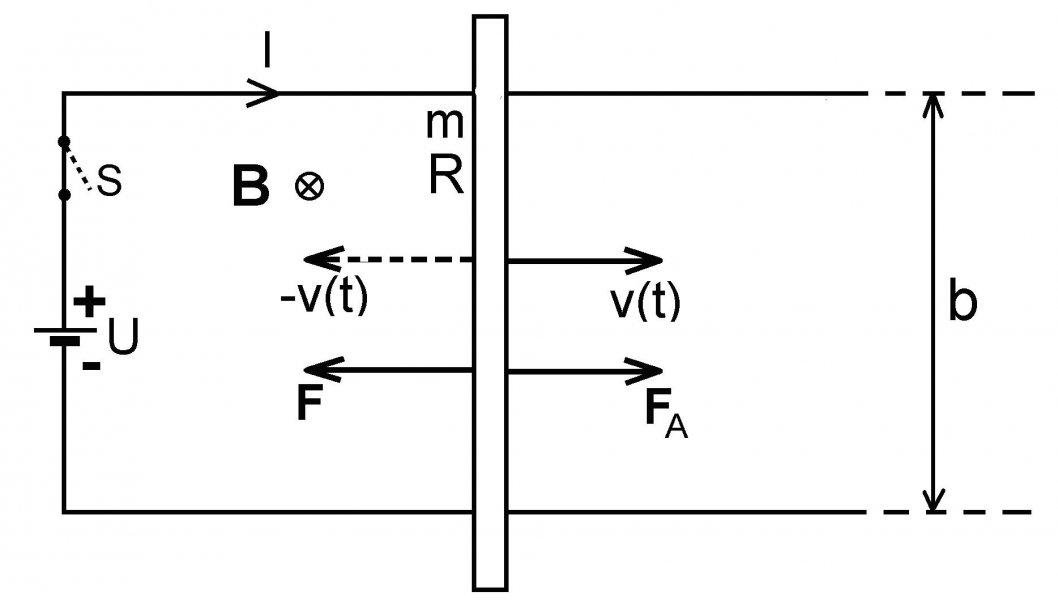
Pozrime sa, čo sa stane, ak nity, ktorými je tyč upevnená odstránime a potom zopneme spínač S (obr. 3). Uvoľnená tyč pod účinkom Ampérovej sily FA(t) = I(t)bB má tendenciu pohybovať sa doprava. Lenže situácie nie je až taká jednoduchá, pretože pri pohybe tyče v magnetickom poli vznikne v nej okamžite ďalšia sila, sila elektromagnetickej indukcie veľkosti Fi(t) = Qv(t)B, smerujúca proti prúdu v obvode (Q je celkový pohybujúci sa náboj v tyči a v(t) je rýchlosť s ktorou sa tyč pohybuje). Účinkom sily elektromagnetickej indukcie vznikne na tyči indukované EMN Ui(t) = v(t)bB s polaritou proti polarite zdroja U.
Obr. 3
Pretože náš obvod je v podstate jednosmerný lineárny elektrický motor s nezávislým budením, pôsobí v ňom obyčajne ešte ďalšia vonkajšia sila F (na obr. 3 brzdná sila F smerujúca doľava). Pod účinkom hnacej elektrickej sily Fe, ktora v tyči smeruje nadol, Ampérovej sily FA a sily elektromagnetickej indukcie Fi (v tyči smeruje nahor), ktorá ovplyvňuje prúd v obvode a teda spätne aj Ampérovu silu FA, sa bude tyč pohybovať. Pozrime sa ako! Napíšme pohybovú rovnicu, pre rýchlosť v(t) tyče
mdv(t)/dt = FA(t) – F = I(t)bB – F,
kde prúd I(t) v obvode je daný rovnicou
I(t)R = U – Ui(t) = U – v(t)bB.
Po dosadení za I(t) v pohybovej rovnici a jej úprave dostaneme
mdv(t)/dt + (b2B2/R)v(t) = UbB/R – F.
V reči matematiky je to obyčajná nehomogénna diferenciálna rovnica prvého rádu s konštantnými koeficientami pre rýchlosť tyče v(t). Z jej tvaru vidieť, že rýchlosť v(t) bude exponenciálne stúpať k asymptotickej, ustálenej hodnote
v = U/(bB) – RF/(b2B2).
(pre jej určenie položme v diferenciálnej rovnici dv(t)/dt = 0 a vypočítajme ustálenú rýchlosť v(∞) = v). Doba, za ktorú sa rýchlosť ustáli na hodnotu v je nekonečná, ale prakticky sa to stane za päťnásobok relaxačnej doby (časovej konštanty)
t´ = mR/(b2B2),
čo v praxi býva dosť rýchlo. Časová konštanta t´ je doba, za ktorú exponenciálny priebeh narastie na (1 – e-1)-tinu svojej stacionárnej hodnoty, čo predstavuje asi 63 % tejto hodnoty (e – základ prirodzených logaritmov), alebo doba za ktorú klesajúci exponenciálny priebeh klesne na e-1-tinu svojej počiatočnej hodnoty (je to asi 37 % počiatočnej hodnoty – pozri napr. nižšie umiestnený obr. 4). Po uplynutí päťnásobnej doby t´sa priebeh od stacionárneho líši iba o cca 7 promile. Odporúčam čitateľovi pozrieť v citovanej učebnici riešenie podobnej úlohy 213, v ktorej úlohu vonkajšej sily hrá gravitačná sila.
Ako vidíme, ustálená rýchlosť tyče v závisí od veľkosti vonkajšej sily F:
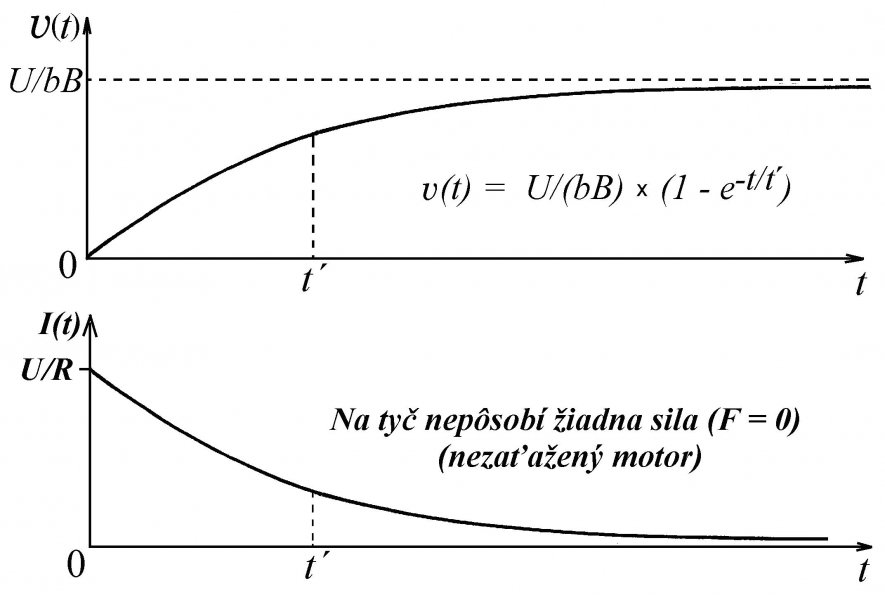
1. Ak F = 0, rýchlosť je maximálna v = U/(bB), čo je prirodzené, motor je nezaťažený (pozri obr. 4).
2. Ak sila F → Fhr = bBU/R, čo je hraničná sila, potom ustálená rýchlosť v → 0, tyč by sa vôbec nepohybovala, indukované napätie by bolo rovné nule. V tomto prípade zdroj EMN dodáva do obvodu konštantný prúd U/R a výkon zdroja sa spotrebuje v odpore R (tyč sa ohrieva).
3. Ak sila F > Fhr, potom smer rýchlosti v je opačný ako smer Ampérovej sily FA a z elektrického motora sa stáva generátor (tento stav z našej úvahy vylúčime).
Obr. 4
1. V prípade ak F = 0 (prípad nezaťaženého elektromotora). Metódu variácie konštánt dostaneme riešenie diferenciálnej rovnice v tvare
v(t) = [U/(bB)](1 – e-t/t´).
Prúd v obvode
I(t) = U/R – (bB/R)v(t) = (U/R) e-t/t´
z hodnoty U/R exponenciálne klesá k nule (pozri obr.4). V ustálenom stave sa v obvode, indukuje EMN Ui = vbB = U, teda rovné EMN zdroja U, ale s opačným znamienkom. Energia zdroja sa v takom prípade spotrebuje na teplo v odpore R s časovo závislým výkonom P(t) = UI(t), ktorý s časom tiež klesá k nule. V ustálenom stave sa v obvode žiaden výkon nespotrebúva.
Treba ešte pripomenúť, že pri zopnutí spínača S v obvode prúd na obr. 4 a následne aj 5 nemôže v okamžiku narásť na nenulovú hodnotu U/R, bráni tomu malá, ale existujúca počiatočná indukčnosť L obvodu. Samoindukcia obvodu spôsobí, že prúd v obvode v skutočnosti nabehne spojite, pritom ale dosť rýchlo a tak prechodový jav po zapnutí na stacionárnu činnosť motora nemá prakticky vplyv.
2. Najdôležitejší je prípad, ak na tyč pôsobí záťažová sila F < Fhr (ale väčšia ako nula – stačí ak je to iba trenie na zberniciach, alebo v guľkových ložiskách pri rotačnom motore). Po vyriešení diferenciálnej rovnice pre v(t), pre prúd v obvode dostaneme
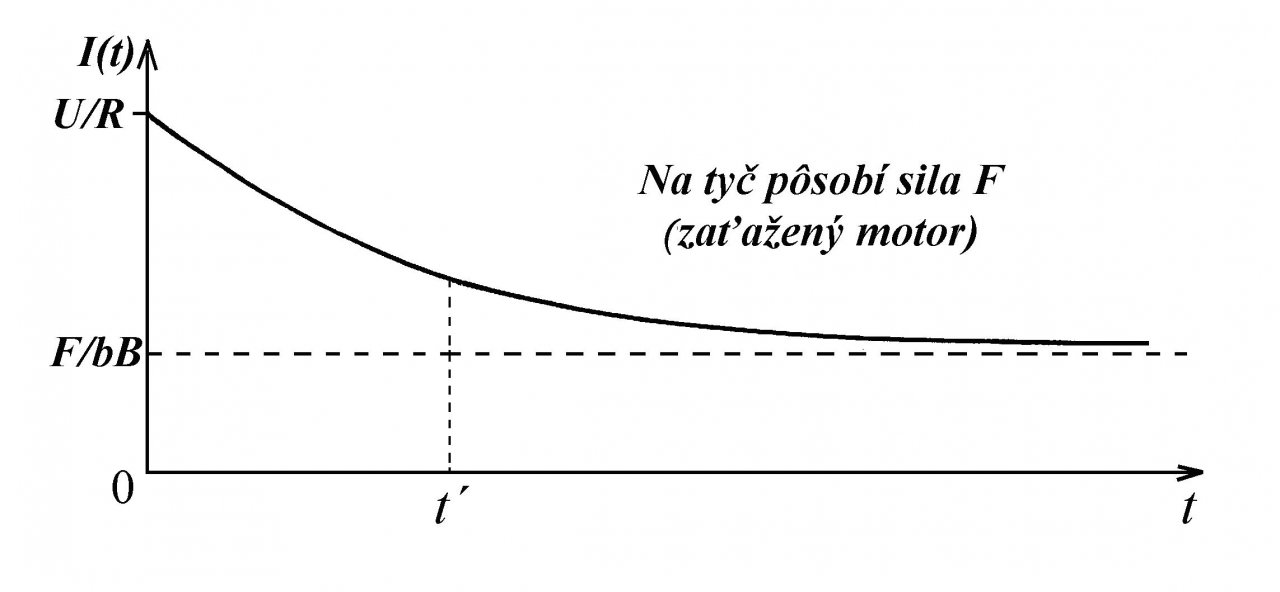
I(t) = [U/R- bBv(t)/R] = (U/R) e-t/t´ + [F/(bB)](1 – e-t/t´).
Obr. 5
Priebeh prúdu odpovedajúci tomuto výrazu je zobrazený na obr. 5. Maximálna hodnota počiatočného prúdu bude taká istá ako u nezaťaženého motora, teda U/R a konečná, ustálená hodnota
I∞ = F/(bB), (1)
kedy Ampérova sila FA = I∞bB a vonkajšia sila F sú v rovnováhe. V priebehu rozbehu tyče (motora) prúd klesá, ale nie k nule, ale k hodnote I∞. Je to veľmi zaujímavý výsledok, podľa ktorého ustálený prúd v obvode nezávisí ani od zdroja EMN U, ani od odporu v obvode R, iba od pôsobiacej brzdnej sily F, a od hodnoty magnetickej indukcie B! Príkon zdroja EMN, dodávaný do celkovej záťaže (do tyče) je
P = UI∞ = UF/(bB) (2)
a je úmerný brzdiacej sile F, čo sa dalo očakávať.
Príkon zdroja EMN v obvode (v tyči)
P = UI∞ = PR + PA, (3) sa skladá z dvoch časti: Je to výkon s ktorým sa časť energie zdroja premieňa na teplo
PR = RI∞2 = RF2/(bB)2, (4) a zvyšok
PA = UI∞ – RI∞2 = UF/(bB) – RF2/(bB)2 = [UF/(bB)](1 – F/Fhr) = vF = Pe (5) je výkon magnetickej Ampérovej sily FA, ktorá koná prácu proti vonkajšej sile F. Na druhej strane, v prúdovom obvode sa tento výkon prejavuje ako výkon indukovaného elektromotorického napätia Ui, teda Pi = UiI∞ = vbBI∞ = vF = UF/(bB) – RF2/(bB)2 = PA (6)
a je rovnaký (lepšie povedané ten istý) ako výkon Ampérovej sily PA, ibaže tu je vyjadrený ako výkon pôsobiaci proti prúdu v obvode. Táto rovnosť výkonov sa využíva k tvrdeniu, že magnetické sily nikdy nekonajú prácu, že totiž rozdiel výkonov (5) a (6) (alebo celkový výkon) sa rovná nule, teda
PA – Pi = 0, (7) čo je síce matematicky správne, ale je to rozdiel tých istých výkonov, iba ináč interpretovaných a tvrdenie (7) má asi takú hodnotu, ako tvrdenie, že 1 m – 100 cm = 0.
Z posledných výrazov vidieť, že výkon Ampérovej sily PA, ako aj výkon indukovaného elektromotorického napätia Pi sú rovnaké a rovnajú sa výkonu zdroja EMN U zmenšeného o tepelný výkon na odpore R tyče, teda Pe = UI∞ – RI∞2 a tak PA = Pi = Pe. (8
O Ampérovej sile a jej výkone v magnetickom pôsobení sa tvrdiť, že je to výkon zdroja EMN Pe. V poriadku, veď v elektromagnetizme máme ako jediný zdroj elektromagnetických pôsobení elektrický náboj a magnetické pole je jedným z jeho prejavov. Bez magnetického poľa B by sa však vyššie uvedené energetické transakcie nemohli uskutočniť, je na to potrebná Ampérová magnetická sila FA = I∞bB. Na prvý pohľad je kuriózne, že ak sila F = 0, celkový výkon P = 0, pritom vtedy v = U/bB, teda je nenulová. Ak sila F sa blíži k hraničnej hodnote Fhr = bBU/R, potom v → 0 a magnetický výkon PA → 0 (preťažený motor). Výkon zdroja sa spotrebuje na teplo v odpore. Ak odpor tyče R → 0, potom aj tepelné straty v systéme (v tyči) PR → 0 a hraničná sila by rástla nad všetky medze. Všetok výkon by sa spotrebovával na prácu magnetickej sily FA. To je samozrejme ideálny, nereálny prípad. Nakoniec si možno ešte všimnúť, že výkon magnetickej sily sa rovná nule, ak záťažová sila F sa rovná nule, ale aj vtedy, keď F = Fhr, čo znamená, že funkcia PA(F) musí mať extrém. Ľahko sa zistí, že extrém je pri hodnote F = Fhr/2, kedy prúd v obvode má hodnotu I∞ = U/(2R). Príkon zdroja v obvode je vtedy P = UI∞ = U2/(2R). Tento príkon sa delí na polovicu: PR = U2/(4R) sa spotrebuje v odpore a PA = U2/(4R) sa spotrebuje ako výkon magnetickej – samozrejme Ampérovej sily. V elektrotechnike je to známy prispôsobený režim, alebo prispôsobená záťaž (matched load) – pozri napr. odsek 5.5 v citovanej učebnici.
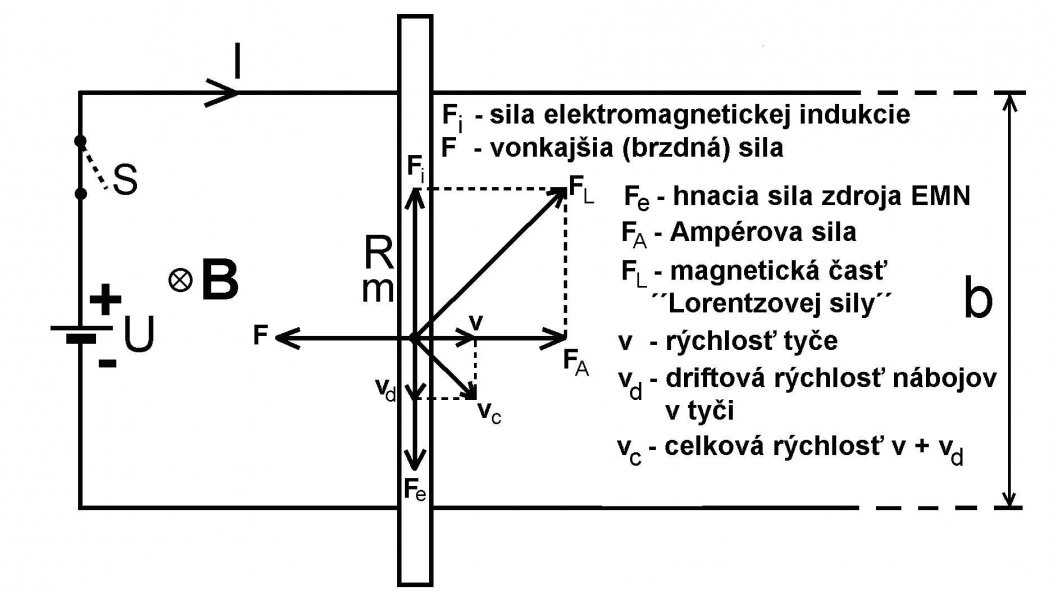
Poďme sa nakoniec pozrieť na silové pôsobenie v našom obvode čisto z hľadiska silových diagramov. Na obr. 6 sú nakreslené všetky sily a vektorové rýchlosti v ustálenom stave, teda po utlmení všetkých prechodových javov, ktoré sme vyššie analyzovali (v zátvorkách je udaná výkonová bilancia – zdrojom dodaný, resp. záťažou spotrebovaný výkon). Ustálený stav sa v praxi dosiahne rýchlo. Rýchlosť tyče v a driftová rýchlosť nábojov vo vodiči vd sú konštantné, to znamená, že sily v ich smeroch sú vykompenzované. Ampérová sila FA = I∞bB (spotrebovaný výkon PA = Pi) je vykompenzovaná silou F (ten istý spotrebovaný výkon PA = Pi) a tyč sa pohybuje konštantnou rýchlosťou v doprava. Prácu teda na tyči koná Ampérova, prízvukujem, magnetická sila, na účet energie zdroja EMN. Aby táto sila existovala, musí v obvode tiecť elektrický prúd I∞ = F/(bB), teda náboje v obvode sa musia pohybovať konštantnou, driftovou rýchlosťou vd (kladné náboje v tyči smerom dole a rýchlosť vd je pri veľkej koncentrácii nosičov nábojov neporovnateľne menšia ako rýchlosť tyče v). To je zaručené rovnosťou elektrickej sily Fe (dodaný výkon ideálnym zdrojom EMN P, mínus stratový výkon v odpore PR, teda celkovo výkon Pe = P – PR), ktorá ženie náboje v obvode a sily elektromagnetickej indukcie Fi (spotrebovaný výkon Pi = PA), ktorá indukuje v tyči protinapätie vbB. Ináč povedané sila Fe je jedina sila spojená s dodávaním výkonu zdrojom EMN, ktorá v galvanickom článku vzniká v dôsledku elektrochemických pochodov, zmenšená o „brzdnú silu“ odporu R. Tento zložitý kolotoč síl a výkonov v konečnom dôsledku vedie k odovzdaniu výkonu zdroja EMN P z časti do záťaže PA = Pi, ktorú reprezentuje sila F a z časti do odporu R, teda PR a nakoniec P = PA + PR = Pi + PR.
"Lorentzova sila"
Nakoniec tu máme ešte jednu, kontraverznú silu – Lorentzovu silu FL (pozri obr. 6 – v tejto úvahe pod Lorentzovou silou rozumieme iba magnetickú časť všeobecnej Lorentzovej elektromagnetickej sily). Treba povedať, že na všetky otázky okolo práce magnetických síl sme dostali odpoveď aj bez Lorentzovej sily, ktorá tu robí viac škody, ako úžitku. Ako sa píše v literatúre, táto sila nekoná žiadnu prácu, pretože je kolmá na neobvyklý, ale možný súčet rýchlosti vc = v + vd. Neobvyklý preto, lebo rýchlosť vd závisí aj od rýchlosti v. Na základe tohto výroku sa vo fyzike po celom svete traduje názor, že magnetické sily nikdy nekonajú prácu. V ďalšom si dovolím k tomuto tvrdeniu vysloviť svoje výhrady:
1. Ako prvý argument za to, že magnetická energia a teda aj magnetické sily prácu konajú, je prechodový jav RL podľa obr. 1, kde magnetická energia uložená v magnetickom poli solenoidu vykonala tepelnú prácu na odpore R. Tu skutočne niet nič iného, okrem magnetického poľa, čo by túto prácu vykonalo.
2. Silu FL na obr. 6 možno rozložiť na jej zložky FA a Fi (ak nie je to naopak, že práve ona je súčtom týchto zložiek, čo je rozdiel!). Teda
FL = FA + Fi = FA – Fe pretože Fi = – Fe. Súčet výkonov týchto síl sa má rovnať nule, takže PL = FL.vc = (FA – Fe).(v + vd) = FAv – Fevd = PA – Pe = 0, z čoho plynie, že PA = Pe (tie sú nenulové!), alebo slovne, že výkon PA Ampérovej sily sa rovná výkonu Pe, s ktorým zdroj EMN dodáva do systému energiu. Takto vykonštruovaná sila dáva správnu energetickú bilanciu, ktorá už je vyjadrená výrazmi (7) a (8) bez silových diagramov a Lorentzovej sily. Tu sa na prvý pohľad zdá, že magnetické pole z tejto energetickej bilancie úplne vypadlo, ale domnievam sa, že nie je to pravda, pretože Ampérova (magnetická!) sila je daná výrazom FA = I∞bB a teda bez magnetického poľa by k tejto energetickej výmene nemohlo dôjsť
3. Možno povedať, že magnetická Ampérova sila FA prácu (resp. výkon, teda prácu za jednotku času) koná. Je hradená z energie zdroja EMN, ale nie je možné ju vykonať bez prítomnosti magnetického poľa. Zavedená Lorentzova sila FL naopak, prácu nekoná. Elektroinžinierov ale zaujíma magnetická Ampérova sila FA. Je preto vágne tvrdenie, že magnetické sily nikdy nekonajú prácu.
4. Možno dokonca vysloviť „kacírsky“ názor, že celá analýza Lorentzovej sile v elektrických strojoch pracujúcich s magnetickým poľom je zavádzajúca a nemá žiadny praktický význam, pretože s takou silou konštruktéri elektrických strojov nepracujú (dokazali sme to v predchádzajúcich riadkoch). Je skutočne dobrá na to, aby sa mohlo vyhlasovať, že magnetické sily nekonajú žiadnu prácu a pritom je to pravda iba vtedy, keď magnetická sila pôsobí na voľný náboj, ktorý koná kruhový pohyb, a nie na prúdovodiče. Slnko tiež nekoná nijakú prácu na planetách, ktoré okolo neho obiehajú. Vidno to aj z toho, ako ťažko, zložito a nepresvedčivo sa táto magnetická sila v iných prípadoch zdôvodňuje. Pre prax sú dôležité vyššie napísané vzťahy (1) až (8), ktoré súvisia s výkonom a prácou – samozrejme Ampérovej magnetickej sily.
5. Závažná okolnosť, ktorá svedči proti sile FL, ako Lorentzovej sile, je skutočnosť, že na celej tyči má stále ten istý smer a to bez ohľadu na to, kde sa tyč práve pohybuje. Aj rýchlosť vc (kolmá na FL) sa tiež všade zachováva. Ako potom takáto sila môže centrálne pôsobiť? Zdá sa, že sila bola vymyslená umelo a cielene – nie sila FL určuje pohyb nábojov, ale náboje s tyčou určujú smer tejto kontraverznej sily (tu sa totiž príčina zamieňa s následkom)!!! Takáto Lorentzova sila vyvoláva vo mne zmiešané pocity.
6. Ako argument svedčiaci v prospech zavedenie Lorentzovej sily sa môže zdať výraz PA = Pe, ale tento výsledok bol odvodený vyššie – sú to výrazy (7) a (8) - bez potreby silových diagramov a Lorentzovej sily (nakoniec aké odvádzanie!) Môže sa tiež vyskytnúť otázka, ako je možné, že pri nesprávnej interpretácii Lorentzovej sily vyšiel správny energetický výsledok PA = Pe. Je to tým, že výraz je správny v tom zmysle, že súčet uvažovaných síl je kolmý na vytvorenú rýchlosť vc a výkony týchto síl sú čo do veľkosti rovnaké!
7. Je ešte jeden veľmi závažný praktický argument proti vyššie zavedenej Lorentzovej sile. Rýchlosť pohybu náboja vo vodičoch (driftová rýchlosť vd) je neporovnateľne nižšia ako rýchlosť pohybu vodičov v pri elektromagnetickej indukcii, teda vd « v. Napríklad ak medeným vodičom polomeru r = 0,5 mm tečie relatívne veľký prúd I = 1 A, potom pri koncentrácii voľných nosičov náboja v medi n = 8,5.1028 m-3 (elektróny s absolútnou hodnotou náboja e = 1,602.10-19 C), driftová rýchlosť elektrónov je iba vd = I/(n.e.pi.r2) = 9,36.10-5 m/s (pi = 3,14159..... je Ludolfovo číslo) a teda vc ≈ v (pozri napr.odsek 5.1.1 citovanej učebnice). Skonštruovaná Lorentzová sila bude mať teda prakticky smer a veľkosť sily elektromagnetickej indukcie vo vodiči, ktorá je daná vektorovým súčinom ~ v × B, ale o tejto sile nemožno tvrdiť, že nie je spojená s prácou.
Treba si ale uvedomiť, že malá driftová rýchlosť je zanedbateľná iba v súčte rýchlosti v+vd, na ktorú Lorentzova sila je kolmá, nie však pri tvorbe prúdu, alebo prúdovej hustoty vo vodiči, kde táto malá rýchlosť vd vystupuje v súčine s obrovskou koncentráciou n voľných nosičov náboja e, to znamená súčinu vde n a táto výsledná prúdová hustota, alebo odpovedajúci prúd môžu mať veľké hodnoty. To iba znovu dokazuje, že zavedená Lorentzova sila je tu nevhodná.
8. Na druhej strane – jednoznačne možno povedať, že na voľnom náboji, pohybujúcom sa rýchlosťou v kolmo na smer magnetického poľa, magnetická sila FL nekoná žiadnu prácu, je dostredivou silou, iba zakrivuje jeho dráhu a núti ho pohybovať sa po kružnici daného polomeru s danou cyklotrónovou frekvenciou, čo už bolo viackrát konštatované. Táto skutočnosť plynie aj z hlbšieho princípu minimálneho účinku. O Ampérovej sile v tejto súvislosti nemožno hovoriť.
9. Možno tiež položiť otázku, či vonkajšie magnetické pole je iba pasívnym prostredníkom prenosu energie zo zdroja do záťaže, alebo či sa nejakým spôsobom na prenose energie zúčastňuje aj vlastnou energiou. Ak je vonkajšie pole produktom napr. veľkého solenoidu s istou indukčnosťou L1, potom náš obvod s vlastnou indukčnosťou L2 a indukčnosť solenoidu L1 vytvárajú vzájomnú indukčnosť M = k(L1L2)1/2, kde k je koeficient väzby obvodov, ktorý môže nadobúdať hodnoty od 0 po 1 a to môže viesť k vzájomnému prenosu energie (pozri odsek 7.5.1 citovanej učebnice), ale to už sú otázky, ktoré sa vymykajú z rámca našich úvah a sú veľmi vzdialené Lorentzovej sile. Treba si tiež uvedomiť, že pole B je tiež produkt nejakého prúdu, alebo permanentného magnetu, takže tieto otázky sú naozaj neobyčajne zložité a nemožno ich vybaviť jednoduchým prehlásením, že magnetické pole prácu nikdy nekoná. V každom prípade svoju úlohu tu hrá aj filozofia prístupu k problému.
10. Ak magnetické pole je produktom permanentných magnetov, často sa objavuje otázka, ako je možné, že magnet nestráca svoje magnetické pole pri interakcii s elektrickými prúdmi napr. v situáciach podobných tým v predchádzajúcich prípadom. Treba povedať, že k demagnetizácii magnetov dochádza, ale vo väčšine praktických prípadov je táto demagnetizácia nepatrná a závisí od kvality magnetu, presnejšie povedané od jeho koercitívnej intenzity. Moderné feromagnetické zliatiny, ako napr. zliatina neodým-železo-bór má koercitívnu intenzitu takmer 1000 kA/m a magnety vyrobené z týchto materiálov sú neobyčajne odolné proti demagnetizácii. Principiálne aj túto magnetizáciu možno ovplyvňovať, napríklad dostatočne veľkým demagnetizačným prúdom, ohriatím na vysoké teploty alebo aj mechanicky, napríklad úderom kladivom na magnet.
Nerád sa odvolávam na autority, ale tu urobím výnimku. Dodatočne som si prečítal záver k tejto problematike v učebnici spolunositeľa Nobelovej ceny za Čerenkovov efekt I. E. Tamma: Osnovy teorii električestva (Základy teórie elektriny), GITTL Moskva 1957, kde koniec §76 znie: pri pohybe vodiča v magnetickom poli práca ponderomotorickej sily tohto poľa sa veľkosťou rovná práci elektromotorickej sily, indukovanej vo vodiči, v dôsledku pohybu vodiča v tomto poli, pritom znamienko ponderomotorickej sily je opačné. „Poetomu polnaja rabota sil magnitnogo polja ravna nulju“. (Poslednú vetu prekladať netreba; – ponderomotorická sila, v našom poňatí Ampérova sila FA, je mechanická „váhová“, presnejšie „záťažová“ sila – pondus, lat. = tiaž, závažie, váha, ponderomotorický = pohybujúci, hýbuci hmotnými telesami)!!! Tamm tvrdí iba toľko, že celková práca (súčet, alebo rozdiel tých istých prác) sa rovná nule, čo nie je to isté ako nulová práca, kedy sa nič nedeje. Domnievam sa, že odtiaľ pochádzajú tvrdenia v sovietskej literatúre o nulovej práci magnetických síl, pretože všetky sú na jedno kopyto..
*****
Výsledky vyššie urobenej analýzy možno z energetického hľadiska porovnať so situácia zobrazenou na obr. 1. Tam zdroj EMN odovzdával tepelný výkon odporu a súčasne zvyšoval magnetickú energiu indukčnosti L. Po ustálení prechodového javu zdroj dodával do odporu konštantný výkon pri konštantnom prúde, teda PR = I∞2R a v solenoide (indukčnosti L) uložil konštantnú energiu Wm = (1/2) LI∞2 = (1/2) FiI∞ (prepínač v polohe 1). Ak by solenoid vťahoval do dutiny napr. železné, feromagnetické jadro, ktoré by bolo brzdené, musel by zdroj dodať väčší prúd, čo by sa prejavilo aj na tepelnom výkone v odpore R.
Zaujímavé javy vzniknú v obvode na obr. 3, ak je zdroj EMN z neho vyradený, nahradený skratom, a tyči je udelená počiatočná rýchlosť v0. Tyč sa bude zotrvačnosťou istý čas spomalene pohybovať, čo vyvolá v tyči vznik indukovaného EMN, v obvode potečie prúd, ktorý bude tyč ohrievať. Taká úloha je riešená v citovanej učebnici (úloha 196). V úlohe 214 v obvode bez zdroja EMN v magntickom poli vonkajšou silou je gravitačná sila.
Obr. 7 Obr. 8
Nakoniec pridávam ako pochúťku čitateľom obrázky 7 a 8 - perokresby (C.A.Faber) dvoch prekrásnych jednosmerných elektromotorov, ktoré vyrábali nemecké firmy Oerlikon a Esslingen v druhej polovici devätnásteho storočia, teda ešte v Maxwellovych a Faradayovych časoch. Prvý pracoval s príkonom 625 V × 270 A ~ 169 kW. V motoroch priam vidieť ako v magnetickom poli statorov (štyri resp. dva póly elektromagnetov produkujúcich statické magnetické pole B kolmo na rotor - kotvu) pôsobí Ampérova (magnetická!) sila FA točivým účinkom na rotor (tangenciálne okolo rotora). Prúd I = 270 A tečie v závitoch rotora (počet kolektorových lamiel 200) popred póly elektromagnetov v smere osi rotácie rotora (magnetická indukcia B neznáma). Odpor kotvy R = 0,025 ohmov. Magnetická Ampérova sila FA takto vykonáva v motore mechanickú prácu! (Obrázky a údaje prevzaté z knihy Holzt A.: Die Schule des Elektrotechnikers, Verlag von Moritz Schäfer, Leipzig 1896). Všetkým mojím čitateľom, hlavne tým, čo sa prebojovali až sem, ale aj tým ostatným, želám krásny deň! Autor
07.08.2009
28. Skutočne magnetické sily nikdy nekonajú prácu ? - (2)
Úvahy o magnetických silách a práci magnetických síl chcem ukončiť troma úlohami, v ktorých znovu chcem poukázať na podiel magnetických síl pri energetických premenách v elektrických obvodoch. V prvých dvoch úlohách je ten istý obvod s tyčou, ako v úvahe 27, ale zdroj EMN bude z obvodov odstránený a nahradený odporom R. Naopak tyč bude v obidvoch prípadoch ideálne vodivá. V prvej úlohe sa tyč bude pohybovať v magnetickom poli pod účinkom gravitačnej sily. V druhej úlohe dostane tyč mechanický impulz (hybnosť) a bude sa pohybovať bez účinku gravitačnej sily. V poslednej, tretej úlohe v rovnakom obvode pôsobí zdroj EMN a treba vypočítať rýchlosť tyče a dodaný výkon do obvodu.
Vo všetkých úlohach pôsobiaca magnetická indukcia B = 1 T je veľmi silné magnetické pole (v jednotkách CGSM je to pole 10 000 gaussov (G), alebo 10 000 oerstedov (Oe) – píšem to tu iba preto, že niektorí starší na to ešte nezabudli a mladší sa s tým možu stretnúť v starých učebniciach). Pre porovnanie, maximálna magnetická indukcia na zemských magnetických póloch je iba cca 6,2.10-5 T = 0,62 Oe. Magnetické pole 1 T je tak veľké, že sa v bežných feromagnetických elektromagnetoch ani nedá dosiahnuť (pozri napr. „Elektromagnetizmus“, kapitola 8). Nuž, nechajme hovoriť úlohy!
Obr. 1 Obr. 2
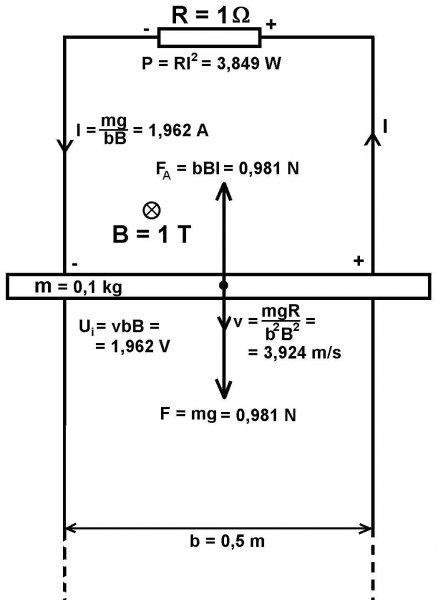
Úloha 1: Po dvoch vertikálnych vodičoch vo vzdialenosti b = 50 cm spojených hore odporom R = 1 ohm sa môže bez trenia a bezodporovo kĺzať tyč hmotnosti m = 0,1 kg (obr. 1), inač všetky vodiče včítane tyče sú ideálne vodivé. Obvod sa nachádza v magnetickom poli indukcie B = 1 T, kolmom na rovinu obvodu. Nájdite ustálenú (maximálnu) rýchlosť v, ktorú nadobudne vodič pri svojom páde v gravitačnom poli Zeme. Aký ustálený prúd pritom potečie obvodom? Aký tepelný výkon sa spotrebuje v odpore R?
Riešenie: Keď sa tyč v magnetickom poli uvoľní, začne sa v gravitačnom poli pod účinkom gravitačnej sily F = mg pohybovať rýchlosťou v(t) nadol (pozri obr. 1). Treba dopredu povedať, že všetky numerické údaje na obrázku sú ustálené hodnoty. Na tyči okamžite vznikne indukované EMN Ui(t) = v(t)bB, ktoré v obvode tvorenom tyčou a odporom R vybudí prúd
I(t) = Ui/R = v(t)bB/R
a tento vyvolá Ampérovu silu
FA(t) = I(t)bB = v(t)b2B2/R
smerujúcu nahor. Na tyč potom pôsobí výsledná sila F(t), ako rozdiel síl F – FA(t) smerom nadol, teda
F(t) = F - FA(t) = mg - v(t)b2B2/R.
Pre pohyb tyče možno napísať pohybovú rovnicu
mdv(t)/dt = F(t)
z ktorej po dosadení za F(t) a úprave dostaneme diferenciálnu rovnicu
mdv(t)/dt + (b2B2/R)v(t)= mg.
Jej riešením je exponenciálne narástajúca rýchlosť v(t) od nuly ku konečnej, ustálenej hodnote, s časovou konštantou t´ = mR/(b2B2). Keďže nás prechodový stav nezaujíma, ustálenú rýchlosť v tyče dostaneme, ak položíme dv(t)/dt = 0 a tak
v = mgR/(b2B2) = 3,924 m/s.
Ustálený stav sa dosiahne za cca päťnásobok časovej konštanty obvodu, čo je
5t´ = 5mR/(b2B2) = 2 s.
Vtedy sa ustálené hodnoty všetkých zobrazených veličín na obr. 1 budú líšiť od skutočných hodnôt iba o cca 7 ‰ (promile). Ustálený prúd v obvode je
I∞ = I = Ui/R = vbB/R = mg/(bB) = 1,962 A.
Nakoniec môžeme urobiť výkonovú bilanciu: Výkon gravitačnej sily v tyči P = Fv = mgv = 3,849 W
indukuje v tyči prúd I = 1,962 A, ktorý vytvára spolu s magnetickým poľom B magnetickú Ampérovu silu FA = bBI = 0,981 N, táto kompenzuje gravitačnú silu F = mg = 0,981 N a pôsobí výkonom
PA = FAv = IbBv = (mg)2R/(bB)2 = RI2 = 3,849 W.
Na tyči sa indukuje napätie Ui = vbB = 1,962 V, s polaritou udanou na obr. 1. Odporu R sa nakoniec odovzdáva tepelný výkon
PT = P = UiI = RI2 = (mg)2R/(bB)2 = 3,849 W,
ktorý sa rovná výkonu P gravitačnej sily F.
Pri riešení úlohy nevznikla potreba zavedenie umelej „Lorentzovej sily“, úmernej súčinu magnetickej indukcie B so súčtom rýchlosti v a driftovej rýchlosti nosičov voľných nábojov v obvode (v tyči). Bola by tu neadekvátna a iba by zahmlila riešenie úlohy. Elektrotechnikov môže prekvapiť, že výkon v odpore stúpa s veľkosťou odporu R, lepšie povedané stúpa s veľkosťou súčinu mR, pretože aj rýchlosť tyče v rastie s týmto súčinom. Pohybujúca sa tyč v obvode, v magnetickom polí, pôsobí ako tvrdý prúdový zdroj nezávislý od odporu R.
Na prvý pohľad by sa mohlo zdať, že padajúca tyč v gravitačnom a magnetickom poli môže byť lacným zdrojom elektrickej energie, ale takú myšlienku treba okamžite zavrhnúť, ak si uvedomíme, že gravitačné pole je konzervatívne pole a práca v ňom po uzavretej dráhe sa vždy rovná nule! Tyč po páde treba totiž zase vyniesť nahor!
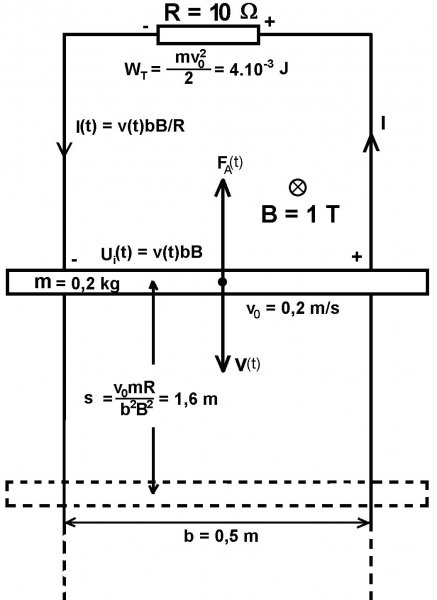
Úloha 2: Kovová tyč s hmotnosťou m = 0,2 kg sa môže bez trenia pohybovať po dvoch paralelných vodičoch uložených horizontálne vo vzdialenosti b = 0,5 m a na jednom konci spojených odporom R = 10 ohmov (obr. 2). Odpor vodičov a tyče je zanedbateľný. Kolmo k rovine vodičov je naložené silné homogénne magnetické pole indukcie B = 1 T. V čase t = 0 je tyči udelená rýchlosť v0 = 0,2 m/s.
a) Určite dobu, počas ktorej sa tyč bude pohybovať.
b) Akú dráhu pritom tyč prejde?
c) Na čo sa premení začiatočná kinetická energia tyče?
Riešenie: a) Pri pohybe tyče vzniká v nej indukované EMN Ui(t) = v(t)bB a v obvode tečie prúd
I(t) = Ui(t)/R = v(t)bB/R
a na tyč bude pôsobiť jediná sila – Ampérova sila
FA(t) = bBI(t) = v(t)b2B2/R
smerujúca proti smeru pohybu tyče. Táto sila je zviazaná s rýchlosťou tyče v(t) pohybovou rovnicou
mdv(t)/dt +v(t)b2B2/R = 0.
Túto diferenciálnu rovnicu možno riešiť separáciou premenných so začiatočnou podmienkou v(0) = v0 v čase t = 0, čím dostaneme pre rýchlosť tyče výraz
v(t) = v0exp(-b2B2t/(mR)) = v0e-t/t´,
kde
t´ = mR/(b2B2) = 8 s
je časová konštanta obvodu. Teoreticky sa tyč sa bude pohybovať nekonečne dlho s exponenciálne klesajúcou rýchlosťou v čase, prakticky jej rýchlosť klesne na nulu (s presnosťou na 7 ‰) za cca 5t´ = 40 sekúnd.
b) Dráha, ktorú tyč prejde, je integrálnym súčtom príspevkov ds = v(t)dt v čase od t = 0 do nekonečna. Táto draha je ale konečná a je daná výrazom
s = v0mR/(b2B2) = 1,6 m.
c) Pohybujúca sa tyč vykonáva prácu proti pôsobiacej sile od magnetického poľa. Táto práca sa vznikom elektrického prúdu I(t) v obvode mení na Joulovo teplo v odpore R. Energia premenená na teplo je súčtom integrálnych príspevkov
dWT = RI2(t)dt = (b2B2/R)v2(t)dt
a po integrácii v čase od nula do nekonečna
WT = mv02/2 = 4.10-3 J
a teda sa rovná začiatočnej kinetickej energii tyče. Práca sa vykoná prostredníctvom magnetického poľa, teda prostredníctvom Ampérovej magnetickej sily, alebo - komu sa to nepáči - prostredníctvom sily elektromagnetickej indukcie, čo je v tomto kontexte to isté.
Kontraverzná "Lorentzova sila" by aj tu mala všade na tyči rovnaký smer a jej veľkosť by s časom a so vzdialenosťou od východzej polohy klesala k nule.
Úloha 3: V obvode na obr. 3, ktorý poznáme z úvahy 27 (jednosmerný lineárny elektrický motor), je zadaný zdroj jednosmerného EMN U = 5 V s vnútorným odporom Ri = 0,1 ohmov. Elektrický obvod uzatvára ideálne vodivá tyč, prepojením dvoch zberníc uložených horizontálne. Tyč sa môže na zberniciach bezodporovo a bez trenia kĺzať. Po zopnutí spínača S, po uplynutí dostatočne dlhého času, bolo meraním ampérmetrom zistené, že v obvode tečie stály prúd I = 4 A a že tyč sa pohybuje konštantnou rýchlosťou v doprava.
Nájdite rýchlosť tyče v a vonkajšiu, brzdnú silu F, ktorá pôsobí proti pohybu tyče. Vypočítajte dodaný celkový príkon P zdroja EMN, tepelný výkon PR na vnútornom odpore Ri zdroja a výkon PA Ampérovej sily FA, ktorý je v rovnováhe s výkonom Pv brzdnej, vonkajšej sily F.
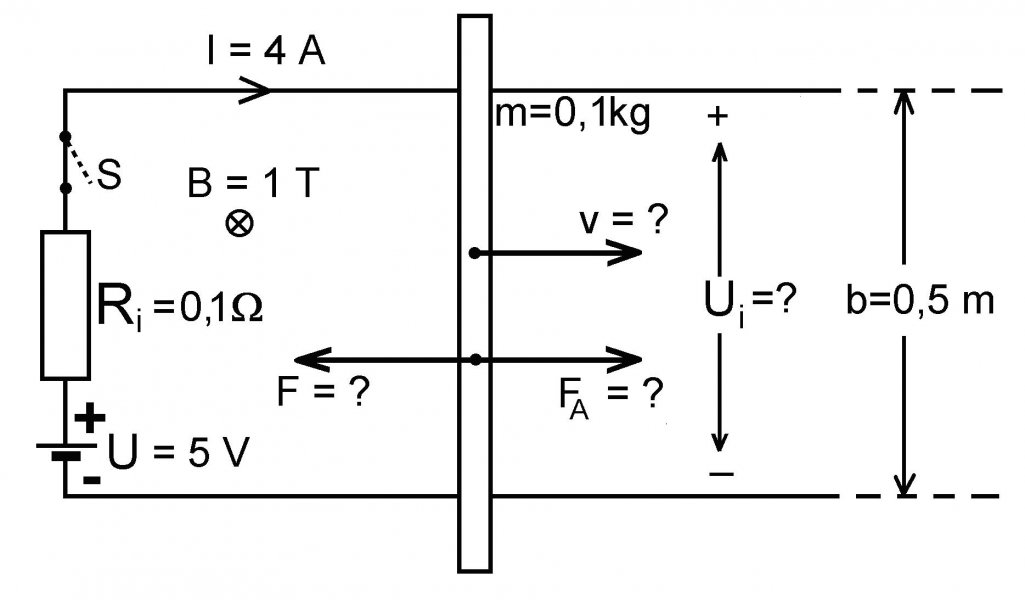
Obr. 3
Riešenie: Po zopnutí spínača S začne v obvode tiecť elektrický prúd ktorý v tyči vyvolá Ampérovu silu. Pod jej účinkom sa tyč začne pohybovať doprava s exponenciálne rastúcou rýchlosťou k asymptotickej hodnote v (pozri úvahu 27). Časová konštanta obvodu
t´ = mR/(b2B2) = 0,04 s,
to znamená, že ustálený stav sa dosiahne asi za 5t´ = 0,2 s.
Pri dosiahnutí ustálenej hodnoty v, prúd v obvode tiež narastie na asymptotickú hodnotu I∞ = I = 4 A a na vnútornom odpore zdroja EMN sa vytvorí potenciálny spád RiI = 0,4 V. Výsledné svorkové napätie zdroja na tyči
Ue = U - RiI = 4,6 V
musí byť kompletne kompenzované indukovaným EMN
Ui = vbB = 4,6 V
v tyči, v dôsledku jej pohybu v magnetickom poli B (odpor tyče sa rovná nule, polarita indukovaného napätia Ui je udaná na obrázku). Z toho pre rýchlosť tyče plynie stála hodnota
v = Ui/(bB) = 9,2 m/s
(čo je cca 33 km/hod). Ampérova magnetická sila, ktorá uvádza tyč do pohybu má veľkosť
FA = bBI = 2 N
a brzdná sila F má rovnakú veľkosť, teda F = 2 N.
Príkon zdroja EMN
P = UI = 20 W,
tepelný výkon na vnútornom odpore zdroja EMN
PR = RiI2 = 1,6 W
(zdroj sa ohrieva). Výkon Ampérovej sily
PA = vFA = 18,4 W
je rovnako veľký ako výkon Pv brzdnej vonkajšej sily F. Všetkým Vám želám pekný a príjemný deň. Autor
23.08.2009
29. Superstabilizácia frekvencie reflexného klystrónu
Nasledujúca úvaha je určená pre čitateľov, ktorí majú isté vedomostí o činnosti mikrovlnových generátorov – predovšetkým o činnosti reflexného klystrónu a polovodičových mikrovlnových generátorov. Ak ich nemajú, a chcú ich získať, odkazujem ich na príručku „Mikrovlnové generátory“ na tejto webovej stránke, v časti „Knihy“. Pre pochopenie úvahy treba predpokladať aspoň stredoškolské elektrotechnické vzdelanie. Samozrejme, že tí, čo majú dosť peňazí a môžu si vysokostabilný mikrovlnový generátor kúpiť, pričom ich nezaujíma fyzikálny princíp činnosti superstabilizácie, môžu si ušetriť čas a úvahu nečítať.

Obr. 1
Na obr. 1 je znázornená štandardná mikrovlnová meracia súprava na ktorej možno vykonávať základné mikrovlnové merania a ktorá je používaná na Fakulte matematiky, fyziky a informatiky UK v Bratislave v rámci predmetu „Praktikum z elektroniky a fyziky tuhých látok“, na magisterskom štúdiu. Neštandardným na tejto súprave je použitý frekvenčne superstabilizovaný napájací zdroj pre reflexný klystrón. Tento superstabilizačný systém bol v šesťdesiatych rokoch uplynulého storočia vyvinutý na Katedre experimentálnej fyziky Prírodovedeckej fakulty UK v Bratislave pri konštrukcii spektrometra elektrónovej paramagnetickej rezonancie (EPR). Žiaľ autorom nebol nikdy publikovaný a tak v odbornej verejnosti upadol do zabudnutia. Udivuje ma, že výrobcovia mikrovlnových generátorov už dávno "neskočili" (a možno aj skočili!) po tomtu vynikajúcom stabilizačnom systéme, ktorý zaručuje relativnú stabilitu frekvencie generátora lepšiu ako 10-7 pri minimálnych výrobných nákladoch. Spoľahlivosť, vysoká účinnosť a stabilita systému bola mnohoročne overovaná v mikrovlnovom praktiku na Fakulte matematiky, fyziky a informatiky UK v Bratislave. Podobný stabilizačný zdroj možno vytvoriť aj pre stabilizáciu frekvencie polovodičových nízkovýkonových mikrovlnových generátorov, napr. Gunnových oscilátorov.
Na stabilitu frekvencie klystrónu sa často kladú vysoké nároky. Tak je to napríklad, ak klystrón je generátorom elektromagnetického žiarenia v spektrometri elektrónovej paramagnetickej rezonancie (EPR). Ako je známe frekvencia generovaného výkonu reflexného klystrónu závisí od prieletového uhla elektrónov v reflektorovom grupovacom priestore a tým od napätia rezonátora U0, ale hlavne od napätia reflektora UR. Stabilná frekvencia predpokladá, že tieto napätia sú vysokostabilné, čo znamená, že zdroje napätia sú elektronicky stabilizované. To však mnohokrát nestačí, pretože frekvencia kmitov klystrónu závisí aj od geometrických rozmerov vnútorného rezonátora klystrónu a tieto rozmery sa so zmenou teploty môžu meniť. K udržaniu extrémne vysokej stability frekvencie možno použiť regulačnú sústavu, v ktorej sa frekvencia klystrónu automaticky dolaďuje na rezonančnú frekvenciu pomocného dutinového rezonátora (vlnomeru) o ktorom – vzhľadom na jeho mechanickú robustnosť – možno predpokladať, že jeho rezonančná frekvencia sa so zmenou teploty takmer nemení (ak aj tieto zmeny prekážajú, treba rezonátor tepelne stabilizovať). Rezonátor – ak je kalibrovaný – sa súčasne používa ako vlnomer na meranie pracovnej frekvencie, alebo vlnovej dĺžky kmitov klystrónu.
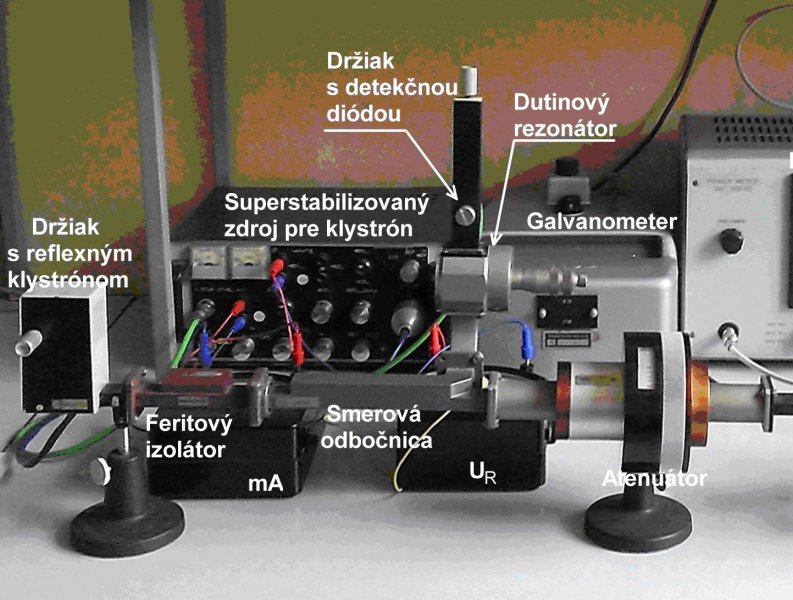 
Obr. 2a Obr. 2b
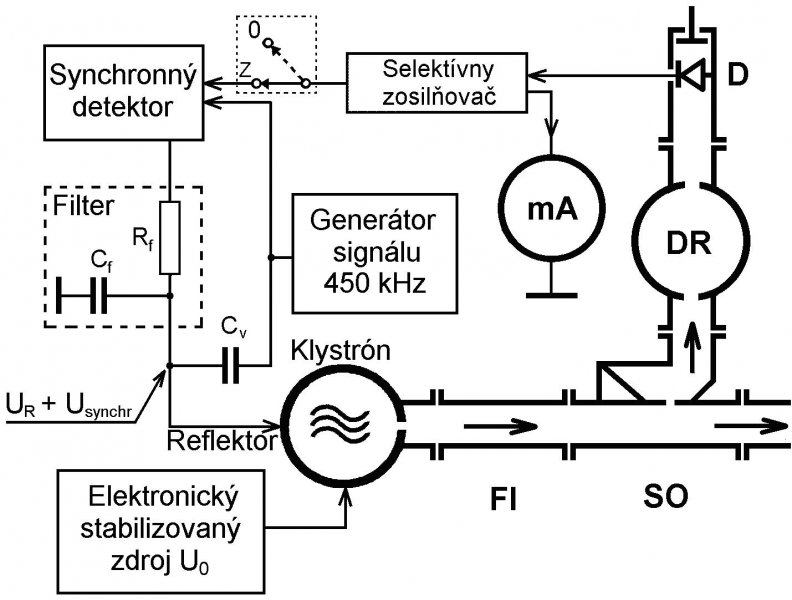
Na obr. 2a je zobrazená časť meracej súpravy v ktorej sa nachádzajú mikrovlnové dielce patriace k obvodom stabilizácie, na obr. 2b je bloková schéma superstabilizácie. Elektronické obvody superstabilizácie frekvencie v našom zariadení sa nachádzajú v spoločnom bloku napájania klystrónu. Podrobná elektrická schéma kompletného zdroja so stabilizačnými obvodmi je uvedená v Dodatku 1 príručky „Praktikum z mikrovlnových obvodov“ uloženej na tejto webovej stránke v časti „Knihy“.
K vytvoreniu slučky superstabilizácie frekvencie treba odbočiť z hlavnej mikrovlnovej trasy malú časť výkonu pomocou smerovej odbočnice SO s odbočným útlmom 10 až 20 dB (obr. 2b). Reflektorové napätie klystrónu UR je modulované vf napätím lokálneho generátora s frekvenciou 450 kHz. Modulačné napätie sa privádza na reflektor klystrónu cez kondenzátor Cv = 68 pF a spôsobí frekvenčnú moduláciu mikrovlnného výkonu na frekvencii 450 kHz.
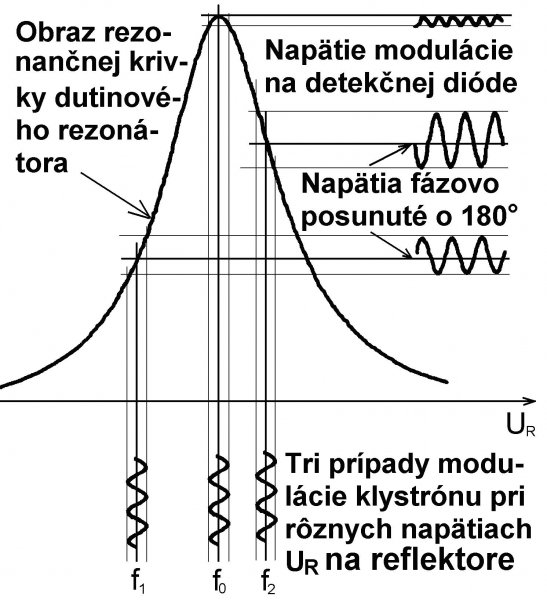
Odbočený mikrovlnový výkon prechádza cez referenčný rezonátor DR a dopadá na detekčnú diódy D. Signál z diódy zosilní selektívny zosilňovač, ktorý je ladený na 450 kHz.Akje rezonátor naladený na frekvenciu klystrónu f0, alebo v jej blízkom okolí, na výstupe detektora je jednosmerné napätie modulované amplitúdovo, s amplitúdou modulácie závislou od frekvencie klystrónu a teda v podstate od reflektorového napätia UR. Ak frekvencia klystrónu je z blízkeho okolia rezonančnej frekvencie referenčného rezonátora, frekvencia modulácie je 450 khz. Ak frekvencia klystrónu sa rovná presne rezonančnej frekvencii rezonátora f0, v tom prípade na dióde je amplitúda modulačného napätia veľmi malá, ale jeho frekvencia je dvojnásobok frekvencie 450 kHz, teda 900 kHz. Táto situácia je zobrazená na obr. 3a.
a) b)
Obr. 3
Predpokladajme, že výstup selektívneho zosilňovača za diódou D na obr. 2b je predbežne rozpojený (výstupný vypínač zosilňovača je v polohe 0) a vyšetríme tri prípady možných hodnôt reflektorového napätia UR (možných hodnôt frekvencie klystrónu), ktoré sú ilustrované na obr. 3a:
1. Klystrón kmitá na frekvencii f0 a na túto frekvenciu je presne naladený dutinový rezonátor (DR v blokovej schéme na obr. 2b). Na výstupe detekčnej diódy D za rezonátorom je napäťový modulačný signál s veľmi malou amplitúdou a s frekvenciou modulácie 2 × 450 kHz = 900 kHz. Tento signál selektívny zosilňovač ladený na 450 kHz za diódou neprenesie a na výstupe zosilňovača je nulové napätie (samozrejme okrem jeho úzkopásmového šumu).
2. Klystrón kmitá na frekvencii f1 nižšej ako je rezonančná frekvencia rezonátora (na ľavej strane od vrcholu rezonančnej krivky). Amplitúda modulačného napätia na výstupe diódy – teraz už na frekvencii 450 kHz – je nenulová a jej hodnota závisí od strmosti rezonančnej krivky pri danom UR (odpovedajúcom f1). Tento signál selektívny zosilňovač zosilní.
3. Klystrón kmitá na frekvencii f2 vyššej ako je rezonančná frekvencia rezonátora (na pravej strane od vrcholu rezonančnej krivky). Amplitúda napätia na dióde a aj na výstupe zosilňovača – pri frekvencii 450 kHz – je nenulová, závislá od strmosti krivky pri hodnote UR(f2). Toto striedavé napätie má ale opačnú fázu, posunutú o 180° oproti fáze napätia v prípade 2.
Takéto možné napätia sa objavia na výstupe selektívneho zosilňovača. V režime stabilizácie sa výstup zosilňovača pripája na vstup synchrónneho detektora (vypínač na výstupe zosilňovača v polohe Z).
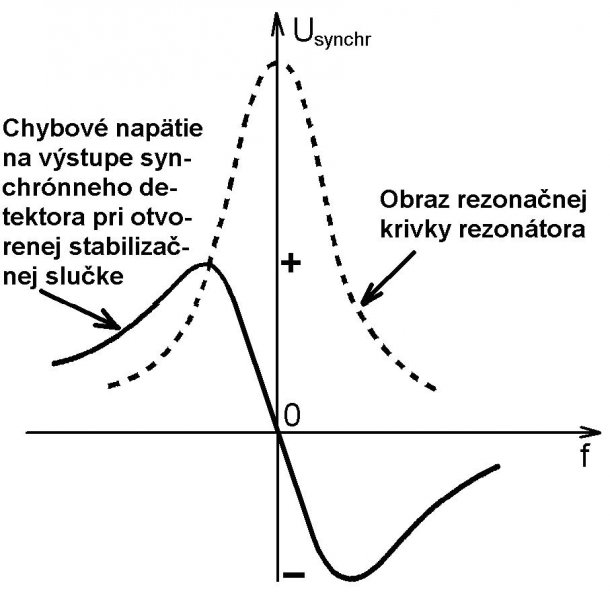
Synchrónný detektor (obr. 2b) je elektronické zariadenie, ktoré násobí dva napäťové signály s rovnakou frekvenciou, ale s rôznou fázou. Výstupný signál synchrónneho detektora je úmerný súčinu amplitúd obidvoch signálov a kosínu ich fázového rozdielu. V našom prípade jedným zo signálov je referenčný signál generátora 450 kHz a druhým je signál na výstupe selektívneho zosilňovača. Signál na výstupe synchrónneho detektora môže byť nulový, alebo nenulový, vo fáze s referenčným napätím, alebo v protifáze, teda fázovo posunutý o 180°. Ak signály sú vo fáze, teda fázový posuv je 0°, cos 0° = 1, potom výstupné napätie synchrodetektora Usynchr je kladné. Ak signály sú v protifáze, teda ak fázový posuv je 180°, cos180° = -1, výstupné napätie Usynchr je záporné. Na výstupe synchrónneho detektora sa teda objaví chybové napätie Usynchr (kladné, nulové, alebo záporné), ktoré po filtrácii má v závislosti od frekvencie klystrónu (od hodnoty UR) priebeh typickej S-krivky (pozri obr. 3b).
Ak napríklad pri rozopnutej slučky frekvencia klystrónu z akýchkoľvek dôvodov poklesne z hodnoty f0, k hodnote f < f0, na výstupe zosilňovača sa objaví signál, ktorý po pripojení na vstup synchrodetektora v správnej fáze, vytvorí na jeho výstupe kladné napätie a to vykompenzuje únik frekvencie. Ak sa frekvencia naopak zvýšila na hodnotu f > f0, na výstupe synchrodetektora sa objaví záporné kompenzačné napätie. Ak je slučka uzavretá, pri akejkoľvek tendencii úniku frekvencie klystrónu (napr. pri zmene teploty klystrónu) regulačná sústava tlačí a udržiava Usynchr na hodnote blízkej nule, čo odpovedá vrcholu rezonančnej krivky rezonátora.
Za synchrónnym detektorom je zaradený dolnofrekvenčný priepust RfCf, ktorý odfiltruje všetky vysoké striedavé zložky signálu. Modulácia frekvencie nutná pre regulačnú sústavu sa prejaví aj v hlavnej vlnovodovej trase a môže v niektorých prípadoch pôsobiť rušivo, preto treba amplitúdu napätia generátora 450 kHz voliť malú. Malá amplitúda striedavého signálu 450 kHz na výstupe detektora D vyžaduje tento signál pred synchrónnou detekciou už spomínaným zosilňovačom selektívne zosilniť.

Obr. 4. Panel superstabilizovaného zdroja pre klystrón
Čo sa týka stability frekvencie, najväčšia chyba (odchýlka frekvencie) pri takejto stabilizácii je úmerná šumovému napätiu na výstupe spätnoväzobnej slučky. Pri zisku spätnoväzobnej slučky 106 ako už bolo uvedené relatívna stabilita frekvencie je rádu 10–7.
Nastavenie sústavy automatickej regulácie frekvencie sa robí po ustálení napájacích zdrojov a teploty klystrónu (pre náročné merania najmenej 20 minút). Pri rozpojenej stabilizačnej slučke (výstup zosilňovača odpojený, na obr. 4 funkčný prepínač na paneli vľavo dole je v polohe 0) sa nastaví reflektorové napätie klystrónu na stred tej triedy kmitania, ktorá poskytuje najväčší výkon. To možno nastaviť napríklad pomocou merača mikrovlnového výkonu v hlavnej trase vedenia. Potom sa ladí piestom rezonátor dovtedy, kým sa neobjaví rezonancia (maximálna výchylka miliampérmetra mA na obr. 1.2a,b). Uzavretím slučky spätnej väzby funkčným prepínačom z polohy 0 do polohy Stab (na obr. 4) je superstabilizácia uvedená do činnosti. Pri ladení rezonátora netreba ho naladiť presne na vrchol rezonančnej krivky, stačí na jej „svah“, po uzavretí regulačnej slučky sa sústava sama dotiahne do vrcholu krivky. O funkčnosti sústavy sa možno presvedčiť napr. tak, že mierne odladíme rezonátor. Stabilizačný systém zareaguje tak, že zmení reflektorové napätie na novú hodnotu (túto zmenu možno pozorovať na meradle UR) a tá odpovedá novej rezonančnej frekvencii rezonátora (obrazne povedané, zmenou polohy piesta rezonátora možno "tiahnuť" frekvenciu klystrónu). Naopak pri pokuse o zmenu reflektorového napätia UR potenciometrom, stabilizačný systém v istom rozsahu drží napätie reflektora nemenné. Všetkým Vám želám pekný jesenný deň. Autor
11.10.2009
30. Niekoľko slov na prelome rokov!
Milí priatelia!
Rok 2009 sa nám už čoskoro stane históriou a ja považujem za vhodne porozmýšľať o ďalšom osude tejto webovej stránky. Je na nej uložených 29 úvah a viac ako tucet učebníc a učebných textov. Podľa počtu návštev stránky (viac ako 13 800 čitateľov asi za jeden a pol roka) a odkazov, ktoré sú veľmi priaznivé sa dá povedať, že webstránka asi splnila, alebo plní očakávania jej čitateľov.
Spočiatku som ani sám nevedel kam úvahy povedú, písal som ich spontánne, bez vopred určeného výberu tém (vlastne to robím aj teraz), bez časového aj obsahového plánu a mali slúžiť iba ako rozšírenie a prehĺbenie problematiky, ktorou sa zaoberajú na stránke uložené učebnice. Okrem toho som chcel udržať kontakt s mojimi čitateľmi. Niektoré úvahy sa však postupne vymkli z rámca bežnej, každodennej fyziky a možno že pre niektorých čitateľov sa stali priťažké. Neviem to posúdiť, pretože negatívne hodnotenia od čitateľov som nedostal. Verím však, že základný cieľ, uvedený v prvej úvahe bol splnený. Či budem v úvahách pokračovať, to závisí od dobrých nápadov, od inšpirácie. Možno že si niektorí čitatelia všimli, že som pozmenil a doplnil aj niektoré staršie úvahy (to je výhoda internetu, že na rozdiel od papierovej informácie možno svoje názory aj korigovať, v horšom prípade zmeniť, alebo v najhoršom prípade dokonca odvolať – ale to som s uloženými úvahami nemusel robiť). S čitateľmi chcem zostať v spojení hlavne prostredníctvom odkazov a na prípadné jednoduchšie otázky sa pokúsim priamo v odkazoch odpovedať.
Chcel by som sa ešte vrátiť k dôvodu vzniku tejto webstránky. K zriadeniu stránky ma inšpirovala moja dcéra, ktorá ju vytvorila, uložila na ňu základné materiály a aj dnes mi pomáha riešiť zložitejšíe softvérové problémy. V predslove k stránke som uviedol, že dávam študentom fyziky a elektrotechniky bezplatne k dispozícii moje knihy, ktoré by ich mohli zaujímať. Do istej miery som urobil z núdze cnosť! Učebnice „Elektromagnetizmus“ a „Elektronika veľmi vysokých frekvencii“ vyšli v jednom vydaní v papierovej forme, prvá v roku 1999 a druhá v roku 2001. Niektoré ďalšie texty, uvedené na stránke vyšli ako vysokoškolské učebné texty (skriptá) na Fakulty matematiky, fyziky a informatiky UK (niektoré v prvých verziách ešte na Prírodovedeckej fakulte UK).
Učebnica „Elektromagnetizmus“, ktorej bola udelená Prémia Literárneho fondu za rok 1999, bola po objavení na knižnom trhu v extrémne krátkom čase rozobraná. Ako autor som bol viackrát čitateľmi oslovovaný a vyzývaný zariadiť jej druhé vydanie. Lenže situácia s vydávaním odborných kníh na Slovensku nie je až taká jednoduchá. Je smutné a nepochopiteľné, že na vydanie vysokoškolskej učebnice používanej na verejnoprávných, teda nie na súkromných univerzitách na Slovensku, si autor musí zohnať sponzorov, teda komusi sa doprosovať a žobrať, ak chce aby sa jeho nikdy nezaplatená práca dostala na pulty kníhkupectiev a do rúk študentov.
  Prvé vydanie knihy "Elektromagnetizmus" spoločne sponzorovala „Vzdelávacia nadácia Jana Husa“ a „Nadácia otvorená spoločnosť“, začo som im ešte aj dnes povďačný. Bez ich finančnej pomoci by nebolo vyšlo ani prvé vydanie učebnice. Ministerstvo školstva SR aj fakulta odmietli poskytnúť prostriedky na jej vydanie. Podľa ich vyjadrení – a to je tiež paradoxné – na podporu vzdelávania na Ministerstve školstva SR vraj nie sú financie! To mi ministerstvo oznámilo písomne a takto neomalene! Pýtam sa: a načo teda financie na ministerstve sú? Hlavne, že sa vo vládnych kruhoch veľmi často hovorí o potrebe neustáleho zvyšovania vzdelávania na Slovensku. Od agentúry KEGA som sa pokúšal po dva roky získať grant, samozrejme neúspešne, dostali takí, čo nič nenapísali a to nikomu neprekážalo. Za prvé vydanie mi vydavateľ zaplatil iba cca polovicu zmluvne dohodnutej autorskej odmeny. Na druhé vydanie sa mi prostriedky už jednoducho nepodarilo zohnať a pravdupovediac ani som nemal chuť sa v tom angažovať, pretože to považujem za osobnú urážku autora. Nadácie mi odkázali, že o študijnú literatúru vysokoškolákov sa má starať MŠ SR a príslušné vysoké školy, v čom s nimi súhlasím. Ak ministerstvo na vydávanie učebníc financie nemá, tak ono by malo iniciatívne hľadať sponzorov na vydanie učebníc, ktoré za to stoja, ja to považujem za jeho povinnosť!
Momentálne je situácia taká, že učebnicu „Elektromagnetizmus“ z tejto webovej stránky používa ako základnú učebnicu k predmetu "elektromagnetizmus", resp. "elektrina a magnetizmus" okrem Fakulty matematiky, fyziky a informatiky UK na stránke
www.dep.fmph.uniba.sk/mambo/
aj Fakulta elektrotechniky a informatiky STU na stránke
http:/kf.elf.stuba.sk/~markos/prednasky/markos_fyzika2_text.php.
a Přírodovědecká fakulta Masarykovej Univerzity v Brne ju v zozname literatúry k predmetu "elektřina a magnetismus" uvádza ako druhú na svojej stránke
Nie je zanedbateľná ani skutočnosť, že na tejto webstránke je uložená aj nemecká verzia učebnice „Elektromagnetismus“, obzvlášť že je to v čase, keď sme už súčasťou Európskej únie.
Niekto môže namietať, že ak existuje elektronická učebnica, netreba papierovú, ale to nie je pravda. Papierová učebnica je stále neoceniteľná, pretože sa s ňou dá robiť to, čo sa s elektronickou, teda s internetovou nedá (napr. robiť si písomné poznámky, uvádzať vlastné označenia, veľmi rýchle sa orientovať a mať ju poruke hocikde, aj tam kde počítač a internetové pripojenie nie je). Elektronická učebnica má tiež svoje prednosti a to predovšetkým v možnostiach jej neobyčajnej variability a v spôsoboch ako vytvoriť knihu s pomerne malou námahou na vysokej výtvarnej úrovni.
Podľa môjho názoru by odborné knihy mali existovať v obidvoch formách a čitateľ by si podľa svojho vkusu a okolnosti mohol medzi nimi vyberať. A okrem toho, aby naše klasické knižnice za niekoľko rokov nezívali prázdnotou. Alebo je ich osud už spečatený?
Nakoniec by som sa mojim čitateľom chcel ešte raz poďakovať za ich priaznivé ohlasy na stránku v odkazoch, s vierou, že svoj záujem o krásnu a elegantnú časť fyziky – elektromagnetizmus – si zachovajú aj v budúcnosti. V novom roku 2010 Vám želám len všetko dobré. Autor
30. 12. 2009
17. 11. 2010
|
